Compute property

The Compute Property modifier assigns property values to particle, bonds, and other elements based on a user-defined mathematical formula. It can also be used to create new particle and bond properties.

The mathematical formula for computing the value for each element can reference existing per-particle or per-bond data, as well as global parameters such as the simulation box dimensions or the current animation time. A list of available input variables is provided in the modifier’s user interface. Additionally, the Compute Property modifier supports computations involving neighboring particles within a defined spherical volume around each particle or which are bonded to the central particle.

The output property

As explained in the introduction on particle properties, certain properties, such as Color or Radius, have special significance within OVITO because they control the visual appearance of individual particles and bonds. Modifying these properties using the Compute Property modifier directly impacts visualization.

For example, you can:

Modify the Position property to move particles.

Assign new values to the Color property to recolor particles dynamically.

Modify the Selection property, creating a selection set like the Expression selection modifier, but with greater flexibility.

Additionally, you can create entirely new properties and use them in subsequent operations within the data pipeline or export them to an output file. To do so, simply enter a custom property name in the Output property field. Note that property names in OVITO are case-sensitive. Standard property names predefined by the software are available in the drop-down list.

List of standard particle properties

List of standard bond properties

List of standard line properties

List of standard vector properties

Vectorial properties

Some particle properties, such as Position and Color, consist of multiple components (XYZ and RGB). When computing such vector properties, you need to specify a separate scalar expression for each component.

Note

The modifier does not support the creation of new user-defined properties with multiple components – only scalar properties or predefined vectorial properties can be created. Use a Python script modifier, which allows to perform NumPy array computations, for more advanced cases.

Selective assignment

If the specified output property already exists, the modifier overwrites it with the newly computed values. However, by enabling the Compute only for selected elements option, you can restrict property assignment to a subset of particles or bonds, preserving existing values for currently unselected elements.

Conditional values

You can also use conditional logic within expressions using the ternary operator ? :. This allows for simple if-else conditions.

For example, to make the particles in the upper half of the simulation box semi-transparent while keeping those in the lower half fully opaque, use the following expression to set the Transparency property of all particles:

(ReducedPosition.Z > 0.5) ? 0.7 : 0.0

For more complex computations that cannot be performed using conditional expressions like this, consider using a Python script modifier, which allows scripting in a real programming language.

Performing computations over neighbors and bonded particles

The Compute Property modifier supports computations that involve the local neighborhood of particles.

The final output value for the \(i\)-th particle is computed as a sum of two terms: a base expression, \(F(i)\), that is evaluated for the central particle \(i\), and a second term, \(G(i,j)\), that is evaluated for each neighboring (or connected) particle \(j\):

\(P(i) = F(i) + \sum_{j \in \mathcal{N}_i}{G(i,j)}\)

../../../_images/compute_property_neighbor_expr.jpg

The expressions for \(F(i)\) and \(G(i,j)\) must be entered separately in the user interface of the modifier.

The set of visited neighbors, \(\mathcal{N}_i\), may be defined in two ways:

By specifying a cutoff radius, \(R_c\), around each particle, within which neighboring particles are considered:

\(\mathcal{N}_i = {j: |\mathbf{r}_i - \mathbf{r}_j| < R_c}\),

By using the bonds between particles. The neighbor term will then be evaluated for each particle that has a bond to the current central particle.

The neighbor term \(G(i,j)\) may depend on property values of the current neighbor \(j\), the central particle \(i\), and the vector connecting the two particles.

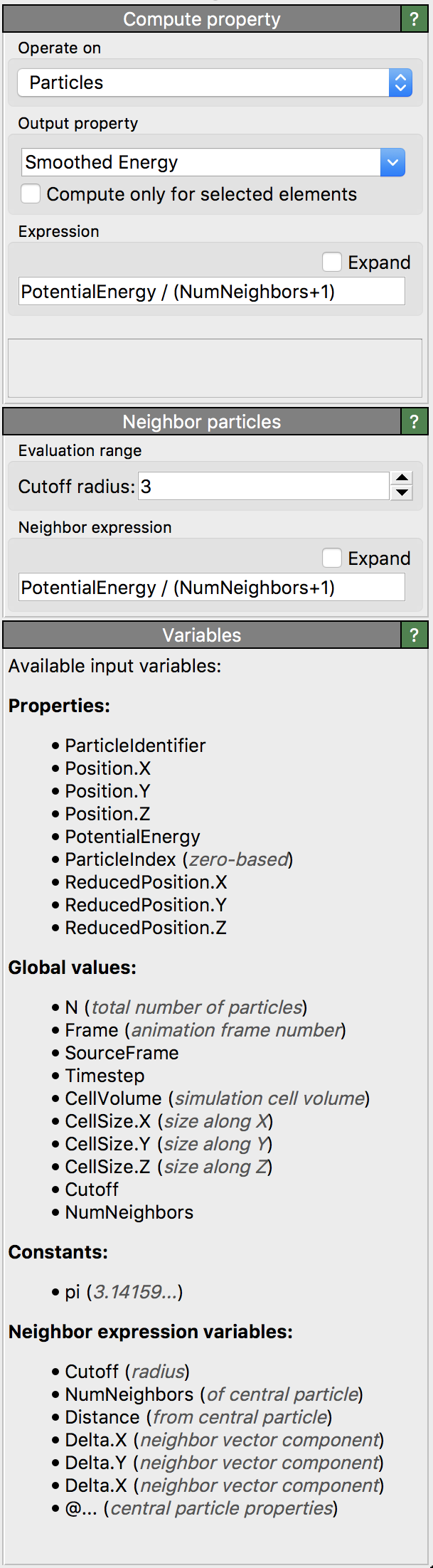
Example: Smoothing a property over neighboring particles

The neighbor expression allows you to perform advanced computations that involve the local neighborhood of particles. For example, you can smooth an existing particle property (e.g. InputProperty) by averaging its value over a particle’s local neighborhood:

F(i)   := InputProperty / (NumNeighbors+1)
G(i,j) := InputProperty / (NumNeighbors+1)

NumNeighbors is a dynamic variable yielding the current number of neighboring particles within the selected cutoff radius, ensuring proper normalization.

Example: Lennard-Jones potential calculation

The following expressions compute the potential energy of each particle using a Lennard-Jones function:

F(i)   := 0
G(i,j) := 4 * (Distance^-12 - Distance^-6)

The dynamic variable Distance in the \(G(i,j)\) expression yields the current separation between the central particle and its neighbor.

Example: Counting neighbor particles of a certain type

The \(G(i,j)\) expression may refer to property values of the central particle \(i\) by prepending the @ prefix to a property name. For instance, the following expressions count the neighbors whose types are different from the type of the central particle:

F(i)   := 0
G(i,j) := (ParticleType != @ParticleType)

Note that the operator != evaluates to 1 if the type of particle \(j\) is not equal to the type of particle \(i\); and 0 otherwise.

Computations on bonds

The modifier can also operate on bonds instead of particles. Then it will compute a new property for each pair-wise bond in the system.

If Operate on is set to Bonds, expression variables refer to existing per-bond properties. You can also include properties of the two connected particles by prefixing their property names with @1. or @2..

For example, to select all bonds that connect different particle types and have a length greater than 2.8, you can set the output bond property to Selection and use the following expression:

@1.ParticleType != @2.ParticleType && BondLength > 2.8

Since bond orientation is arbitrary, @1. and @2. may refer to either connected particle. Thus, to explicitly select bonds between type-1 and type-2 particles, a more complex expression is necessary to account for the two possibilities:

(@1.ParticleType == 1 && @2.ParticleType == 2) || (@1.ParticleType == 2 && @2.ParticleType == 1)

Expression syntax

The modifier’s expression syntax resembles that of the C programming language. Variable names and function names are case-sensitive.

Attention

Spaces in property names are simply left out in the corresponding variable names. For example, the particle property Particle Type is accessible as the variable ParticleType in the expression. Other invalid characters in property names are replaced by underscores in the variable names.

Operators are evaluated in the following order of precedence:

Operator	Description
`(...)`	Parentheses for explicit precedence
`A^B`	Exponentiation (A raised to the power B)
`A*B`, `A/B`	Multiplication and division
`A+B`, `A-B`	Addition and subtraction
`A==B`, `A!=B`, `A<B`, `A<=B`, `A>B`, `A>=B`	Comparisons between A and B (yielding either 0 or 1)
`A && B`	Logical AND: True if both A and B are non-zero
`A \|\| B`	Logical OR: True if A, B, or both are non-zero
`A ? B : C`	Conditional (ternary) operator: If A differs from 0, yields B, else C

The expression parser supports the following functions:

Function name	Description
`abs(A)`	Absolute value of A. If A is negative, returns -A otherwise returns A.
`acos(A)`	Arc-cosine of A. Returns the angle, measured in radians, whose cosine is A.
`acosh(A)`	Same as `acos()` but for hyperbolic cosine.
`asin(A)`	Arc-sine of A. Returns the angle, measured in radians, whose sine is A.
`asinh(A)`	Same as `asin()` but for hyperbolic sine.
`atan(A)`	Arc-tangent of A. Returns the angle, measured in radians, whose tangent is A.
`atan2(Y,X)`	Two argument variant of the arctangent function. Returns the angle, measured in radians. see here.
`atanh(A)`	Same as `atan()` but for hyperbolic tangent.
`avg(A,B,...)`	Returns the average of all arguments.
`cos(A)`	Cosine of A. Returns the cosine of the angle A, where A is measured in radians.
`cosh(A)`	Same as `cos()` but for hyperbolic cosine.
`exp(A)`	Exponential of A. Returns the value of e raised to the power A where e is the base of the natural logarithm, i.e. the non-repeating value approximately equal to 2.71828182846.
`fmod(A,B)`	Returns the floating-point remainder of A/B (rounded towards zero).
`rint(A)`	Rounds A to the closest integer. 0.5 is rounded to 1.
`ln(A)`	Natural (base e) logarithm of A.
`log10(A)`	Base 10 logarithm of A.
`log2(A)`	Base 2 logarithm of A.
`max(A,B,...)`	Returns the maximum of all values.
`min(A,B,...)`	Returns the minimum of all values.
`sign(A)`	Returns: 1 if A is positive; -1 if A is negative; 0 if A is zero.
`sin(A)`	Sine of A. Returns the sine of the angle A, where A is measured in radians.
`sinh(A)`	Same as `sin()` but for hyperbolic sine.
`sqrt(A)`	Square root of a value.
`sum(A,B,...)`	Returns the sum of all parameter values.
`tan(A)`	Tangent of A. Returns the tangent of the angle A, where A is measured in radians.

The parser supports the following constants in expressions:

Constant name	Description
`pi`	Pi (3.14159…)
`inf`	Infinity (∞)

Type names in expressions

Added in version 3.12.0.

Particle types and bond types are represented by unique numeric identifiers in OVITO, i.e., the ParticleType variable evaluates to an integer value uniquely identifying the type of the current particle. The same applies to other typed properties in OVITO such as the Structure Type property.

Each type may have a human-readable name associated with it, e.g., the numeric type 1 may be named “Cu”. You can use these type names in expressions, e.g., ParticleType == "Cu", where the type name is enclosed in double quotes.

For further information on the use of type names in expressions, see here.

Additional examples

Example: Computing particle speed

To compute the linear velocity (speed) of each particle based on the components \((v_x, v_y, v_z)\) of its velocity vector, you can use the following expression:

sqrt(Velocity.X^2 + Velocity.Y^2 + Velocity.Z^2)